2重スリット実験(1)
「物質は、波であり、粒子である」これを、もっとも分かりやすく示してくれる実験が「2重スリット実験」である。
●実験概要
まずは、図をみてほしい。
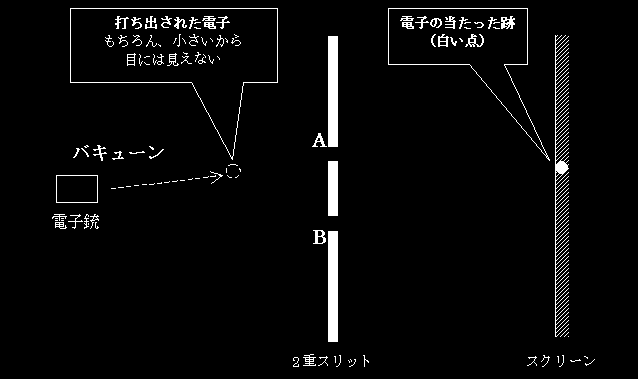
電子銃の前にはボードが置かれ、そのボードには、「2つのスリット(隙間)」を開けられている。そして、ボードの奥には、スクリーンが配置されている。スクリーンは、カメラのフィルムのように感光する性質を持っており、電子が当たると、その場所に白い跡を残す。つまり、スクリーンには、電子が当たった場所が映し出される。これが、2重スリット実験の概要である。
ようするに、2重スリット実験を、一言で言うと、
「2つ穴が開いた板に向かって、電子を飛ばしたとき、その奥のスクリーンに何が映りますか?」
ということである。
●実験開始
さて、2重スリット実験は、電子銃から電子を飛ばして、スクリーンに映ったものを見るだけという簡単お手軽な実験なのだが、電子銃からの「電子の飛ばし方」を変えることで、3種類の実験を行うことができる。
その3種類の実験に、それぞれA、B、Cと名前をつけよう。
●実験A 大量に電子を発射した場合
電子銃から大量の電子を放射してみるとどうなるか。
結論を言うと、スクリーンには綺麗なシマ模様ができる。

これは「干渉縞」である。
(干渉縞については、波派VS粒子派の戦い(1)を参照)
干渉縞ができるのは、「電子が波」だと考えれば、なんの不思議もない。
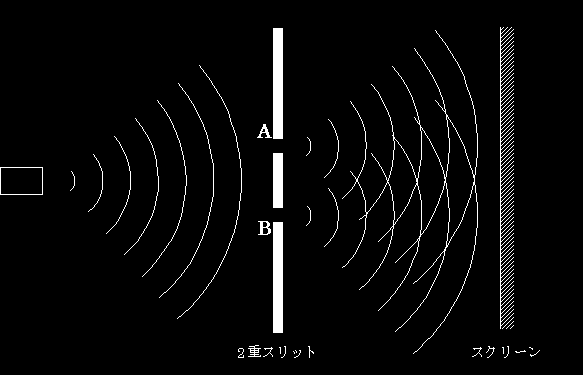
まず、電子銃から、電子の「波」が飛んでいき、ボードに達する。で、ボードには「2つのスリット」があるのだから、波は「スリットAを通っていく波」と「スリットBを通っていく波」の2つに分かれる。
すると、スクリーン上には、その2つの波が重なり合ったものが見えるはずである。
つまり、2つの波の「山と山」「谷と谷」が重なっているところは、お互いに強め合って明るくなり、逆に、波の「山と谷」が重なっているところは、打ち消しあって波が消えてしまい、その場所は暗くなってしまう。したがって、シマ模様を作る。
それだけのことだ。同じことは、海の波を使ってもおきる。
電子が波だと考えれば、何も不思議はない。
●実験B 電子1個を発射した場合
電子銃の出力を小さくして、「電子1個」を発射してみたらどうなるか?
結論を言うと、スクリーンには、ポツンと小さな点が現れる。

これは、電子1個を飛ばしたのだから、スクリーン上には、その1個が当たった場所が「点」として映るということで、当たり前の話である。なんの不思議もない。
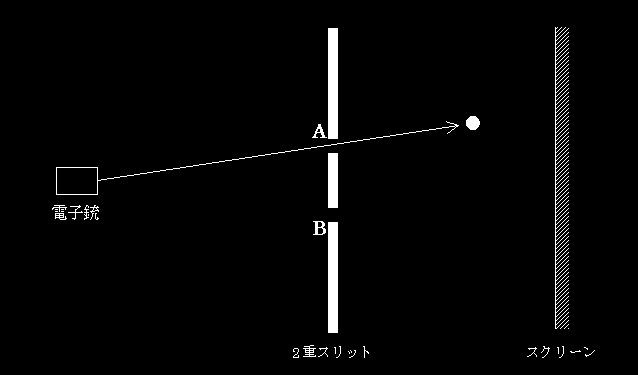
電子が、スクリーン上に「点」として映ることは、「電子が粒子」であるという確かな証拠である。
ちなみに、追加実験として、スリットAとスリットBにそれぞれ、「電子が通ったかどうかを観測するセンサ」を置いてみたとしよう。
もし、電子が本当に粒子であれば、スリットが2つあったら、どちらかのスリットから出て行くはずだ。
(パチンコの玉を想像して欲しい。パチンコの玉が、このボードを越えてスクリーンにたどり着くためには、スリットAかスリットBのどちらかを通り抜けなくてはならない。重要なのは、パチンコの玉(粒子)は、あくまで一方のスリットしか通らないということだ。1個のパチンコの玉が、両方のスリットを通り抜けるということはありえない。
もし、電子が、波であれば、両方のスリットから出て行くかもしれないが、粒子であれば、一方のスリットしか通り抜けないということがミソだ)
さて、2つのスリットに「電子が通ったかどうかを観測するセンサ」を置いて、実際に「電子1個」を飛ばしてみる。すると、2つのセンサのうち、必ず一方のセンサしか反応しないのだ。スリットAのセンサが反応すれば、スリットBのセンサは反応しない。逆に、スリットBのセンサが反応するときは、スリットAのセンサは反応しない。つまり、2つのセンサが同時に反応することはなく、どちらかだけが反応するのだ。
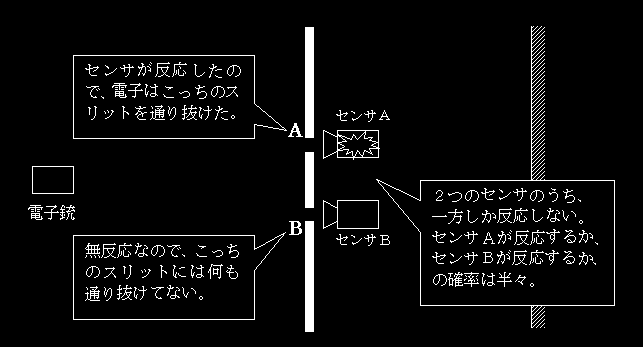
これは、すなわち、電子1個が
「一方のスリットを通り抜けたとしたら、他方のスリットは通り抜けていない」
ということであり、「1個の粒子」であるという確かな証拠である。
1個の粒子が、2つの穴を同時に通り抜けることはありえないので、当たり前の結果だ。
したがって、電子は、粒子であるという結論を持つことができるのだ。
おっとっと。
実験Aでは「電子は波」という結論になり、実験Bでは「電子は粒子」という結論になってしまった。
一体、どっちが正しいのだろうか?










