公理

ユークリッド幾何学とは、我々が、小学校や、中学校で学ぶ幾何学のことだ。ようは、まっ平らな紙の上に描いた「点・直線・平面」などを取り扱う図形の学問のことである。この幾何学の歴史は古く、紀元前３００年頃、エジプトの学者ユークリッドにより体系化された。

では、ユークリッドは、どうやって、この幾何学を作ったのだろうか。
彼は、まず最初に５つの公理を定義し、それらを組み合わせて論理的に考えることで、色々な法則を発見していく、という手法を用いた。

ここで、公理とは、
「証明する必要のない、明らかに自明な法則」のことである。
たとえば、ユークリッド幾何学の5番目の公理は、平行線公理と呼ばれ、まぁ、ようは、「平面上に、絶対に交わらない２本の線（平行線）を引くことができますよ〜」
ということを述べたものである。

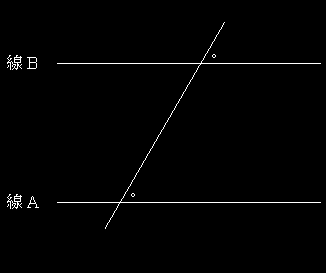
たとえば、下図を見たとき、この線Ａと線Ｂをどれだけ無限に延ばしても、絶対に交わることがないのは、証明するまでもなく、直感的にわかるだろう。


このような「証明する必要もないくらい自明な法則」である公理をもとにして、論理的に考えていけば「三角形の内角の和は、180度である」などの定理が導き出せる。
こういった定理を利用すれば、さらに新しい定理をどんどん発見していくことができ、こうして積みあがった定理の山が幾何学体系というわけだ。

ユークリッド幾何学は、非常に自明な公理をもとにして成り立っており、人間の直感的な理解と一致していたので、幾何学は「正確な客観的事実を記述するもの」と考えられていた。

だが、ちょっと待って欲しい！
ひとつ重大な問題点を見逃してはならない。

公理が自明とは言っても、あくまでも、証明はされていないのだ。
したがって、幾何学は、
証明されていない法則を土台として成り立っているということになる。
だから、もし、本当に、万が一にでも、公理に間違いがあったとすれば、公理から導き出された定理もすべて間違っているということになり、歴史ある幾何学体系は一瞬にして崩壊してしまう。

とはいえ、もちろん多くの人は、
「こんなにシンプルで美しく、何より、客観的な世界を正確に記述できている幾何学に 誤りがあるはずはない」
と考えていたし、
「おそらく、幾何学の公理を勝手に別のものに変えてしまえば、理論体系として矛盾が生じるはずだ。だから、幾何学が理論体系として矛盾がないためには、必然的に今の公理しかありえないのだ」
と考えて、ユークリッド幾何学の公理は絶対的に正しいとされてきた。


しかし、1830年頃、数学の天才ガウスが、この問題に挑んだ結果、なんと、5番目の「平行線の公理」を「平行線も交わる」という公理に置き換えても、幾何学として矛盾が発生せず、それどころかまったく新しい幾何学体系が作られることを発見してしまった。
この幾何学は、非ユークリッド幾何学と呼ばれ、簡単にいえば「歪んだ紙の上に書いた図形」を取り扱うものであり、三角形の内角の和は180度にはならない。

非ユークリッド幾何学は、ユークリッド幾何学とまったく反する公理を用いたにもかかわらず、なんら矛盾が発生しなかったのだ。

これは学問をやっているものにとって、非常にショッキングなことだった。
そもそも。
幾何学のみならず、数学、哲学、ありとあらゆる学問は、ある一定の公理（＝証明は不可能だが、正しいとする暗黙の了解）をもとにして、論理的に組み立てて体系化されたものである。

無から、理論を組み立てることはできない。

どんな理論体系にも、必ず、最初に公理が存在しなくてはならない。

古い時代には、その公理から組みあがった理論体系に矛盾が一切無ければ、その公理も含めて、その理論体系が正しいのだと信じられてきた。しかし、非ユークリッド幾何学の発見により、理論体系の無矛盾性が、公理の「正当性」を表すことにはならず、まったく別の公理に置き換えたとしても、何ら矛盾が起きないことが明らかになってしまった。
（そして、相対性理論による空間の歪みの発見により、むしろ現実に近いのは非ユークリッド幾何学の公理であり、自明だったはずのユークリッド幾何学の公理が、実際には人間の思い込みだったことが明らかになる）

このことの最大の問題点とは、
「適当に、好き勝手に、公理を決めてしまっても、無矛盾な理論体系をいくらでも作り出せる」
ということなのだ。

この事件以降、あらゆる学問の理論体系は「絶対的な真理の記述」ではなくなり、「ある一定の公理）をもとに、論理的思考の蓄積で作られた構造物」とみなされるようになっていった。

そして、それから100年後、ゲーデルが不完全性定理として、

「我々が、どんなに公理を選択して、無矛盾にみえる理論体系を構築しようとも、その理論体系の無矛盾を 自分の理論体系の中で証明することは不可能であるため、選んだ公理が本当に正しいのか証明することは、絶対にできません」

と述べることによって、理論体系は完全にトドメをさされる。