波動関数の収縮

量子力学の通俗本を読むと、必ずと言っていいほど、「波動関数の収縮」という言葉が出てくる。

今回は、この「波動関数の収縮」について、説明してみようと思う。

まず。２重スリット実験をおさらいすると、その結論（コペンハーゲン解釈）は、

「観測していないモノについては、ここにあるかも、あそこにあるかも、という可能性としてしか論じることができない。そして、その言葉どおり、観測していないモノは、『ここにあるかもという可能性』という形で存在している」

というものであった。

もっと端的にいえば、

「観測される前の、電子や原子の位置は、確率的に存在している」

ということである。


さて。
この確率、―つまり、モノが「ここで見つかるかもしれないよ」という確率― の形は、波の形になっている、ということが実験的に確認されている。
（なぜ、そうなるかは、誰もわかっていない。とにかく、実験すると、いつもそういう形になることが確認できるだけだ。）

この波の形は、「波動関数」という数式で記述することができる。波動関数というのは、「波の形」を表現するための方程式だから、波であれば何でも、この方程式で表すことできる。

で、この波動関数が、時間とともに、どう変化していくのかを数式で記述したものが、シュレディンガー方程式だと思って欲しい。

さてさて。
たとえば、ある時刻において、観測されるの前の「電子の位置」は、下図のような「波動関数」で表現することができたとする。



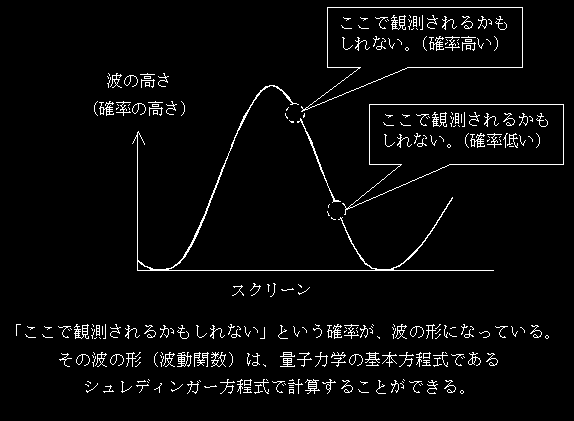
図からわかるとおり、波が高いところほど、電子が観測される確率が高いわけだ。

では観測されたら、この「波動関数」はどうなるか？

今、電子が、たまたま位置Ａで観測されたとする。この観測されたときの状態を、波動関数を当てはめて、無理やり表現してみよう！位置Ａに電子があることはもう確定しているのだから、当然、波動関数の形は、図のようになる。




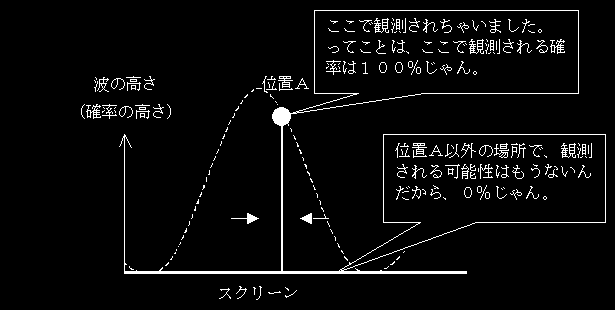
つまるところ、観測によって、電子の位置の波動関数はこのように変わる。




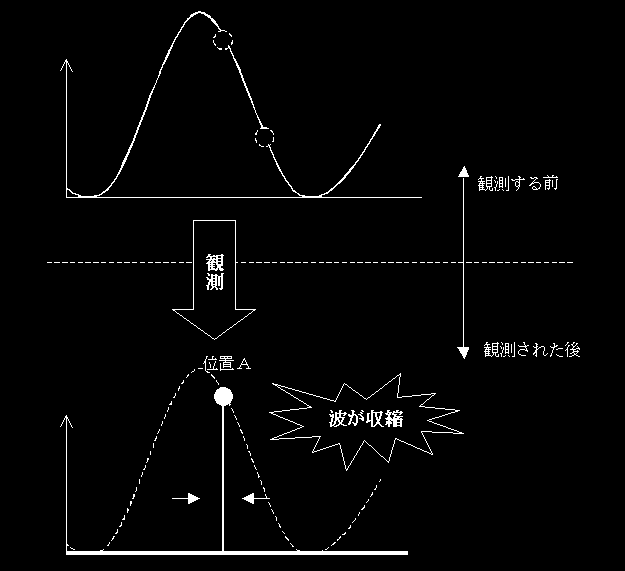
これを、「観測によって、波動関数が収縮した」と表現する。

観測される前までは、「ここらへんにあるかも」って感じで、広がりを持っていた波動関数が、観測された瞬間に、「ここにある！」って感じで、一点に集中している波動関数に変わったのだから、「観測によって、波動関数が収縮した」というのは、まさにそのままの表現だろう。

さて、こうなると、当然、こんな疑問がでてくる。
「ふ〜ん、そうなるのは、わかったけど。でもさ〜、観測すると、なぜ、波動関数が収縮しちゃうの？」

これについて、量子力学の創始者ボーアは、「観測するとなぜ波動関数が収縮しちゃうのか」はっきりさせようとはしなかった。

「え？え？なんで？　ちゃんと、説明してよ。なんでそんな、いいかげんなままなの！」と言いたいかもしれない。

もちろん、多くの人が、「波動関数の収縮」のメカニズムについて、「なぜ、そんなことが起きるのか？」を説明できない量子力学を「不完全な理論だ」と、批判した。

実際、多くの科学者が、量子力学の方程式をがんばってイジクリまわしたが、波動関数を収縮した形にすることはできなかった。結局、「なぜ、観測すると、波動関数がこんな形になっちゃうのか」について、量子力学の方程式では、まったく説明できないのである。

だからよく、量子力学の通俗本では、この「波動関数の収縮」が、「未だ解明されていない謎」として紹介されていたりする。

ではでは、現代の科学者を捕まえて、この「波動関数の収縮」について問い詰めたら、どう答えるだろうか？おそらく、一般人が納得するような答えは返してはくれないだろう。というのは、現代の科学者にとって、「波動関数の収縮」とは、そもそも問題ですらないからだ。

科学において、観測とは、「ナニカから、位置や質量などの物理量（数値）を取り出す操作」である。そして、観測したときに、「どんな物理量（数値）が取り出せるか」を予測することが、科学（量子力学）の仕事なのである。だから、ぶっちゃけ話、「観測した後なんか、どーでもいいのだ」

つまり、「観測が終わったモノに、量子力学（波動関数）を当てはめることが、そもそもナンセンス」なのである。

そもそも、波動関数やシュレディンガー方程式は、
「モノがどこで観測されるかを予測するための道具」「人間が作り出した便利な数式」である。
これらの道具は、観測結果と一致するように、ツジツマを合せて作られただけのものであり、観測されてしまえば、もう関係ないのだ。

使い終わった道具は、捨て去るのみ。

だから、
「観測されると波動関数が収縮する、ことについて、量子力学は何も説明できていない！」
と大騒ぎしても、当の科学側は、

「え？観測されたんでしょ？じゃあ、もういいじゃん？波動関数なんか収縮しないよ。だって、もう使わないもん。とにかく、波動関数という道具を使えば、モノがどこで観測されるのか、その確率を計算でき、実験結果とピタリとあっている。それ以上でも、それ以下でもないけど、ナニカ問題でも？」

という感じなのだ。

「観測されると、波動関数が収縮する、それは一体なぜか？」

科学をやっている人にとっては、この問いかけそのものが、ナンセンスだったりする。

（補足）
しかし、一方で、それを「問題」だと捉えて、一生懸命、考えている科学者もたくさんいる。別の「答え」が見つかるかもしれないのだから、それもまた必要なことであろう。